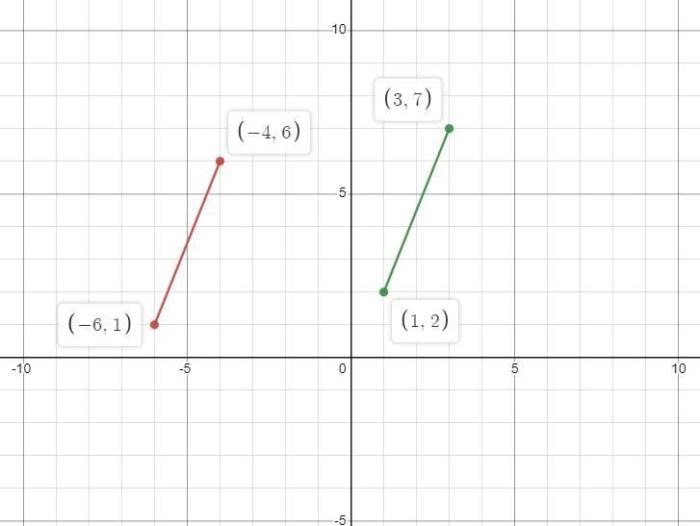
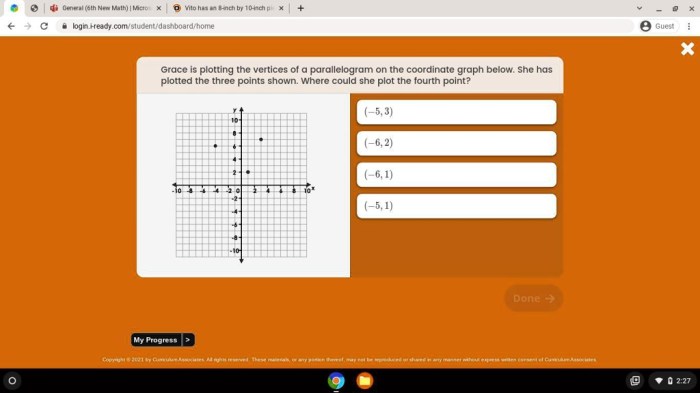
Grace is plotting the vertices of a parallelogram, embarking on a journey that unveils the intricacies of this geometric shape. Delve into the realm of parallelograms, where opposite sides dance in parallel harmony and diagonals intersect with captivating symmetry.
Unravel the secrets of plotting vertices with precision, a skill that unlocks the path to calculating perimeters, areas, and more. Explore the unique properties of parallelograms, such as rectangles, squares, and rhombuses, and witness their applications in architecture, engineering, and beyond.
Plotting the Vertices of a Parallelogram
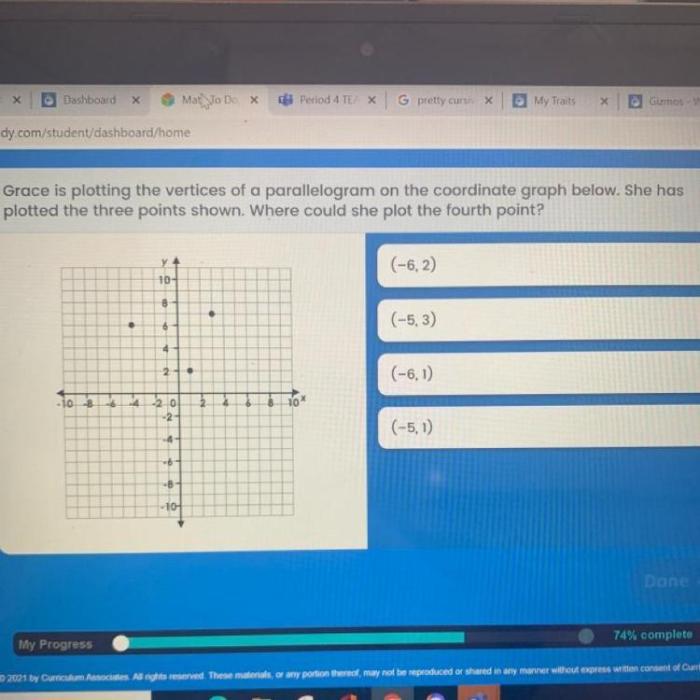
Plotting the vertices of a parallelogram is a crucial step in understanding its geometry and performing subsequent calculations. Accurate plotting ensures that the shape’s dimensions and properties are correctly represented.
To plot the vertices of a parallelogram, follow these steps:
- Determine the coordinates of two adjacent vertices.
- Use the given lengths of the sides to find the coordinates of the opposite vertices.
- Ensure that the opposite sides are parallel by checking if their slopes are equal.
- Verify that the diagonals bisect each other.
Tools such as graph paper, rulers, and compasses can aid in plotting vertices precisely.
Properties of a Parallelogram
Parallelograms possess several key properties:
- Opposite sides are parallel and congruent:This property ensures that the parallelogram has two pairs of equal sides.
- Opposite angles are congruent:The angles opposite each other are equal in measure.
- Diagonals bisect each other:The diagonals of a parallelogram intersect at a point that divides them into two equal segments.
Parallelograms find applications in various fields, including architecture, engineering, and design.
Calculating Perimeter and Area
The perimeter of a parallelogram is calculated using the formula:
Perimeter = 2(Length + Width)
where Length and Width represent the lengths of the adjacent sides.
The area of a parallelogram is calculated using the formula:
Area = Base x Height
where Base represents the length of one side and Height represents the perpendicular distance from the base to the opposite side.
The table below compares the formulas for perimeter and area of a parallelogram with other quadrilaterals:
| Shape | Perimeter | Area |
|---|---|---|
| Parallelogram | 2(Length + Width) | Base x Height |
| Rectangle | 2(Length + Width) | Length x Width |
| Square | 4 x Side Length | Side Length2 |
| Rhombus | 4 x Side Length | (Diagonal1 x Diagonal2) / 2 |
Special Cases and Applications, Grace is plotting the vertices of a parallelogram
Special cases of parallelograms include:
- Rectangle:A parallelogram with all right angles.
- Square:A parallelogram with all sides equal and all angles right angles.
- Rhombus:A parallelogram with all sides equal.
These special cases possess unique properties and applications:
- Rectangles are commonly used in architecture for their structural stability and ease of construction.
- Squares are used in tiling and flooring due to their equal sides and right angles.
- Rhombi are employed in kite making and decorative patterns.
Expert Answers: Grace Is Plotting The Vertices Of A Parallelogram
What are the steps involved in plotting the vertices of a parallelogram?
Gracefully plot the vertices by following these steps: identify two parallel lines, mark congruent segments on each line, connect the endpoints of the segments to form the parallelogram.
How do I calculate the perimeter of a parallelogram?
Embrace the formula: Perimeter = 2(Length + Width), where Length and Width represent the dimensions of your parallelogram.
What is the relationship between the diagonals of a parallelogram?
Diagonals, like graceful dancers, bisect each other at their midpoint, forming a captivating intersection.