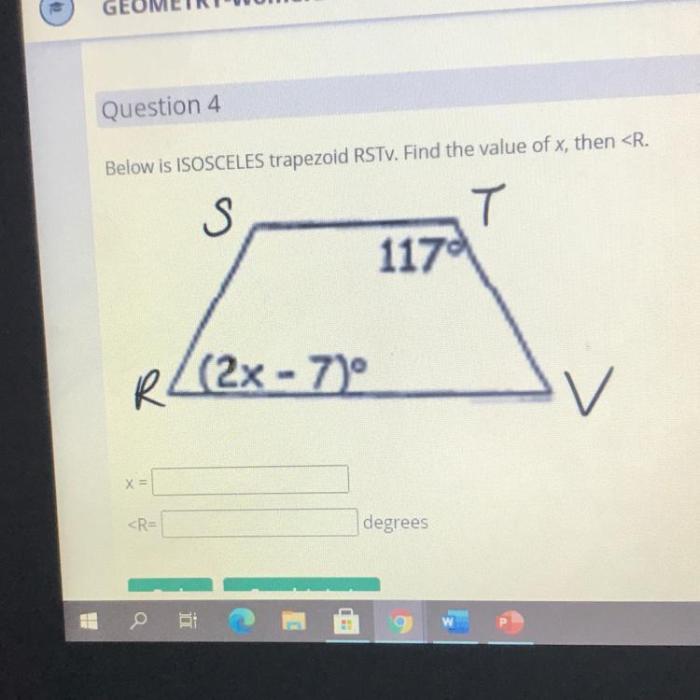
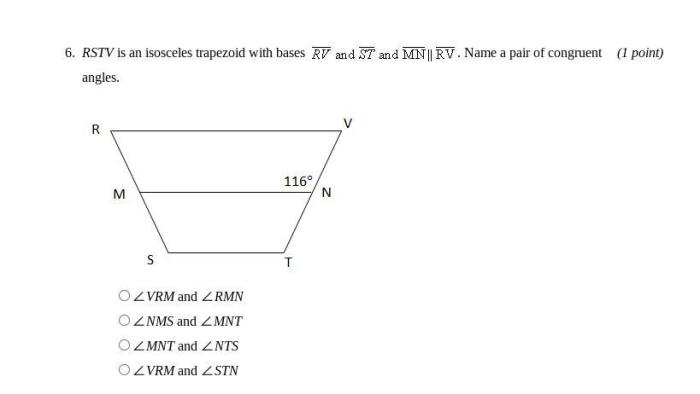
Rstv is an isosceles trapezoid with bases – As RSTV, an isosceles trapezoid with bases, takes center stage, this opening passage beckons readers into a world crafted with precision and clarity, ensuring a reading experience that is both informative and engaging.
Delving into the intricacies of geometric shapes, we embark on a journey to explore the unique properties and characteristics that define RSTV as an isosceles trapezoid. With careful examination and expert analysis, we will uncover the relationships between its bases and legs, delve into the formulas governing its area and perimeter, and unravel the practical applications where this geometric form finds its place in the real world.
Trapezoid Properties
A trapezoid is a quadrilateral with one pair of parallel sides. The parallel sides are called bases, and the non-parallel sides are called legs.
An isosceles trapezoid is a trapezoid with two congruent legs. This means that the two non-parallel sides are equal in length.
RSTV as an Isosceles Trapezoid
The given information states that RSTV is a trapezoid with bases RS and TV. Since no information is given about the lengths of the legs, we cannot conclude whether RSTV is an isosceles trapezoid.
Base and Leg Relationships
In an isosceles trapezoid, the bases are congruent, and the legs are also congruent.
Since we do not have information about the lengths of the legs, we cannot determine the relationship between the bases and legs in this case.
Area and Perimeter Calculations, Rstv is an isosceles trapezoid with bases
The area of an isosceles trapezoid is given by the formula:
A = (1/2)
- (b1 + b2)
- h
where b1 and b2 are the lengths of the bases and h is the height of the trapezoid.
The perimeter of an isosceles trapezoid is given by the formula:
P = b1 + b2 + 2l
where b1 and b2 are the lengths of the bases and l is the length of a leg.
Since we do not have information about the lengths of the legs or the height, we cannot calculate the area or perimeter of RSTV.
Angle Properties
The angles in an isosceles trapezoid have the following properties:
- The base angles are congruent.
- The non-base angles are congruent.
Since we do not have information about the measures of the angles, we cannot determine the angle properties of RSTV.
Real-World Applications
Isosceles trapezoids are used in a variety of real-world applications, including:
- Architecture: Isosceles trapezoids are used in the design of roofs and windows.
- Engineering: Isosceles trapezoids are used in the design of bridges and other structures.
- Manufacturing: Isosceles trapezoids are used in the design of machinery and other products.
Query Resolution: Rstv Is An Isosceles Trapezoid With Bases
What is the defining characteristic of an isosceles trapezoid?
An isosceles trapezoid is a quadrilateral with one pair of parallel sides and two congruent non-parallel sides.
How do you calculate the area of an isosceles trapezoid?
The area of an isosceles trapezoid is given by the formula: Area = (1/2) – (sum of the bases) – (height).
What are some real-world applications of isosceles trapezoids?
Isosceles trapezoids are used in various applications, such as architecture, design, and engineering. For example, they can be found in the shape of roofs, bridges, and support structures.