Solve multi step equations part 1 iready – Welcome to the world of multi-step equations, where solving complex mathematical puzzles becomes an exciting adventure! In this comprehensive guide, we’ll delve into the intricacies of solving multi-step equations part 1 for Iready, equipping you with the knowledge and strategies to conquer any equation that comes your way.
As we embark on this mathematical journey, we’ll explore the fundamentals of multi-step equations, identify the various operations involved, and master the techniques for solving one-step and two-step equations. Along the way, we’ll uncover the secrets of solving equations with variables on both sides, using the distributive property, combining like terms, and factoring.
Define Multi-Step Equations
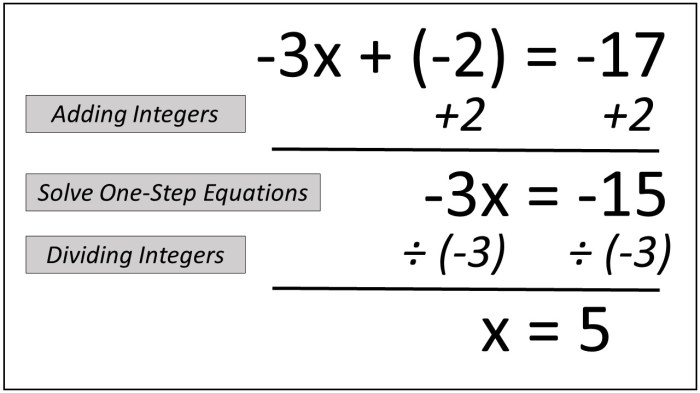
Multi-step equations are equations that require more than one step to solve. They typically involve multiple operations, such as addition, subtraction, multiplication, and division.
Here are some examples of multi-step equations:
- x + 5 = 10
- 2x – 3 = 7
- 3(x + 2) = 15
- x^2 – 4 = 0
Identify Operations in Multi-Step Equations: Solve Multi Step Equations Part 1 Iready

The different operations that can be used in multi-step equations include:
- Addition (+)
- Subtraction (-)
- Multiplication (×)
- Division (÷)
- Exponents (^)
- Radicals (√)
Here are some examples of equations with different operations:
- Addition: x + 5 = 10
- Subtraction: 2x – 3 = 7
- Multiplication: 3(x + 2) = 15
- Division: x/2 = 5
- Exponents: x^2 – 4 = 0
- Radicals: √(x + 1) = 3
FAQ Summary
What are multi-step equations?
Multi-step equations are mathematical equations that require more than one step to solve. They involve multiple operations, such as addition, subtraction, multiplication, and division.
How do I identify the operations in a multi-step equation?
Look for mathematical symbols such as +, -, ×, and ÷. These symbols indicate the operations that need to be performed.
What is the distributive property?
The distributive property is a mathematical property that states that multiplying a sum by a factor is the same as multiplying each term in the sum by the factor.